Research.
I am interested in problems in partial differential equations including global analysis of waves, mathematical relativity and nonlinear waves. My research involves techniques from spectral theory and microlocal analysis.
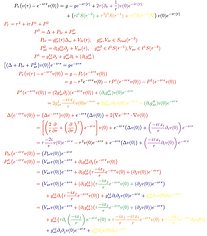
Publications and Pre-prints
Pre-prints
with J. Wunsch. Wave propagation on rotating cosmic string spacetimes. (arXiv link)
Peer Reviewed
-
with J. Wunsch. Mode solutions to the wave equation on a rotating cosmic string background. Proceedings of the AMS. To appear. (arXiv link)
-
with J. Wunsch. Generalized Price's law on fractional-order asymptotically flat stationary spacetimes. Mathematical Research Letters. To appear. (arXiv link)
-
The effect of metric behavior at spatial infinity on pointwise wave decay in the asymptotically flat stationary setting. American Journal of Mathematics. To appear. (arXiv link)
-
with J. Metcalfe. Global existence for systems of quasilinear wave equations in (1+4)-dimensions. Journal of Differential Equations. 2020. (https://doi.org/10.1016/j.jde.2019.09.012)
Thesis
Wave decay in the asymptotically flat stationary setting. 2019, 155 pages. Available from ProQuest Dissertations and Theses Global. (2296357806)
Recent & Upcoming
Talks
For a more expansive list of talks, view my CV
1 / Conferences and Workshops
May Midwest Microlocal Meetings // May 2023
Northwestern University
AMS Central Sectional Meetings // April 2023
University of Cincinnati
PDE Mini-School with Peter Hintz // March 2023
UNC-Chapel Hill
Joint Math Meetings // January 2023
Boston, MA
Harmonic Analysis and Waves // August 2022
University of Washington
Workshop on Microlocal Analysis and PDEs // July 2022
University College London
2 / Seminars and Colloquia
Michigan State University // Dalhousie University // University of Kentucky // Ghent University // Oberlin College
Videos
Generalized Price's law on fractional-order asymptotically flat stationary spacetimes // July 2021
ICMP Young Researchers Symposium
5 minute research introduction // Fall 2019
MSRI
Lecture Notes
MATH 891: Topics Course on Nonlinear Waves // Spring 2017
taught by Jason Metcalfe